微积分初步：函数的变化率
要说在17世纪以前，随便问一个数学家：已知一抛物线与抛物线上一点，怎样求这点处的抛物线切线的斜率？大概你得不到一个准确的回答。但是，微积分能够很好地解决这一问题。
微积分之所以产生主要是当时科学家要研究三类问题：
- 求变速运动的瞬时速度
- 求曲线上一点处的切线
- 求最大值和最小值（ps.这个最大最小可不简单哦）
实际上，这三类问题都可归结为因变量相对于自变量变化而变化的快慢程度，即所谓函数的变化率问题。在真正学习导（数）之前，让我们了解一下函数的变化率罢。
下面是课本定义：
设函数 y=f(x),x∈D,当自变量 x 由点 x₀ 变化到 x₀+Δx 时，相应的函数值由 f(x₀) 变化到 f(x₀+Δx) ，此时 f(x₀+Δx)-f(x₀) 就是相应于自变量 x 改变量 Δx 的函数改变量，比值
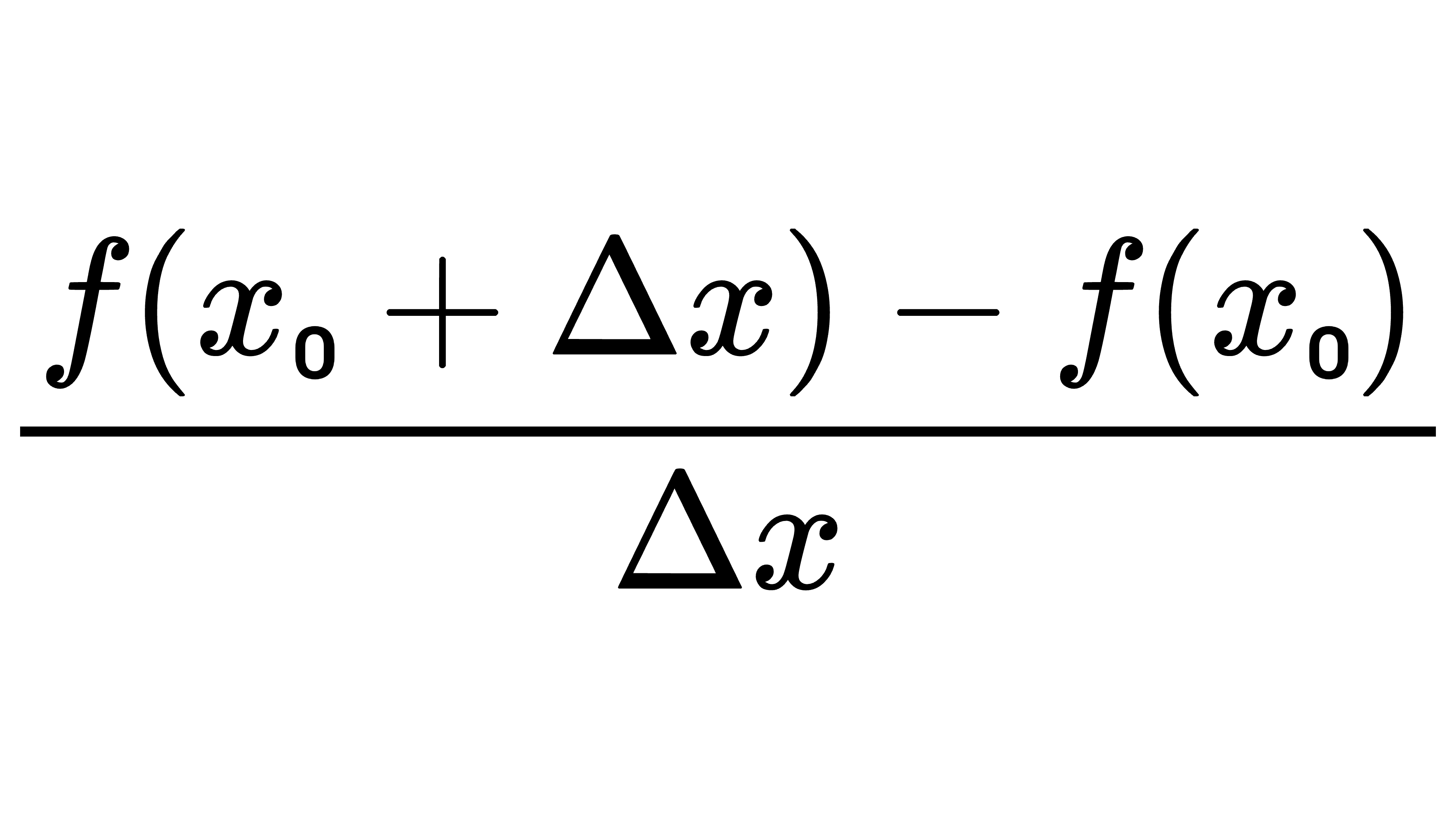
称为函数 y=f(x) 相应于自变量由 x₀ 变化到 x₀+Δx 时的平均变化率，也称为 y=f(x) 在区间[x₀,x₀+Δx]（或[x₀+Δx,x₀]）上的平均变化率，它反应了因变量 y 在以 x₀ 和x₀+Δx 为端点的区间上的平均变化快慢程度。
那么，如果当Δx→0时，平均变化率的极限
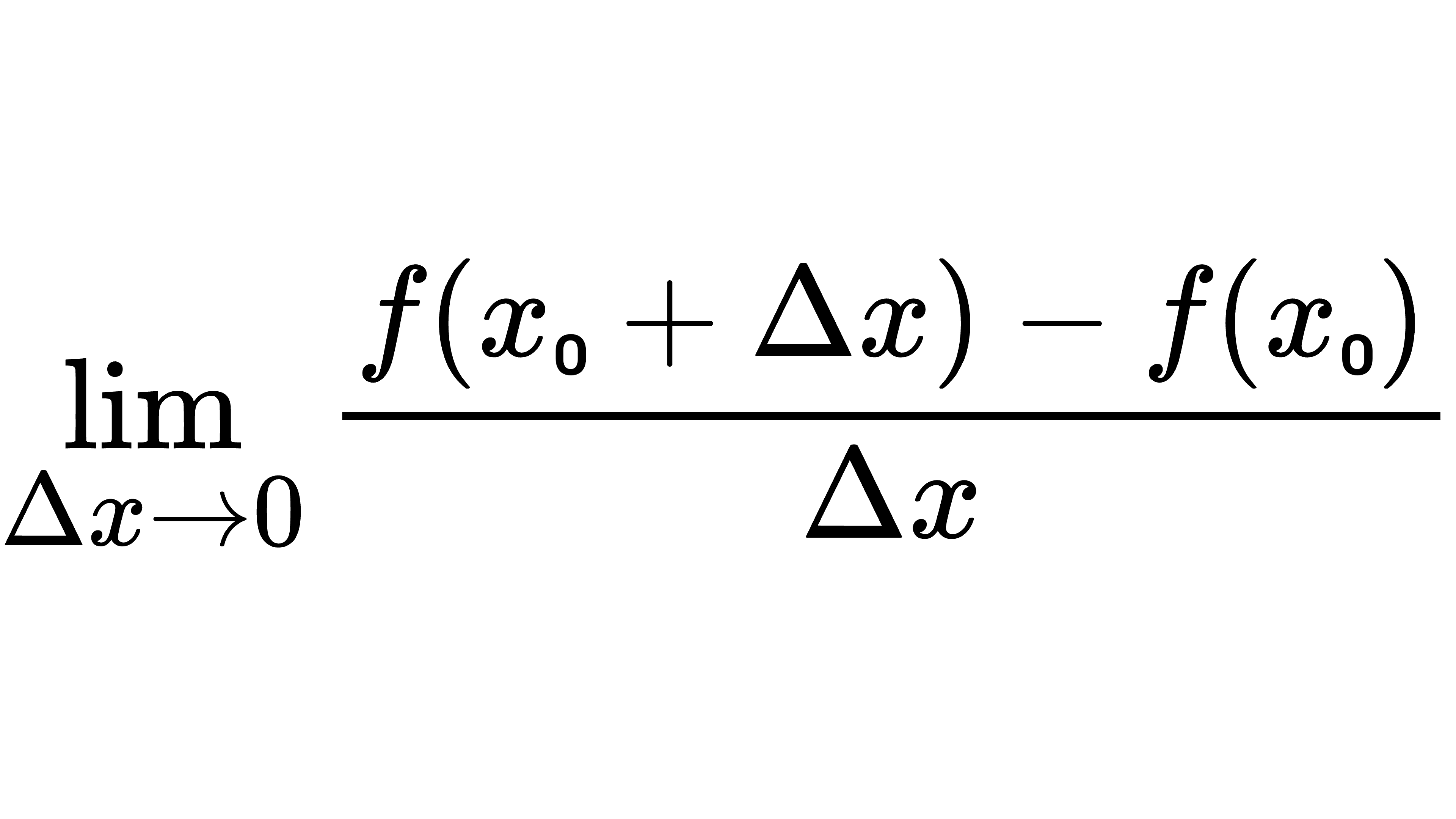
存在，则称此极限值为函数 y=f(x) 在 x₀ 点的变化率，它反应了在 x₀ 点处因变量 y 随自变量的变化而变化的快慢程度。
这样看起来有点不好懂，我们可以举个例子：
一个微笑着的普通男人沿平直公路做变速直线运动，路程为s，运动时间为t，s=s(t)。
很明显，当时间由t₀变到t₀+Δt时，这位普通男人通过的距离为
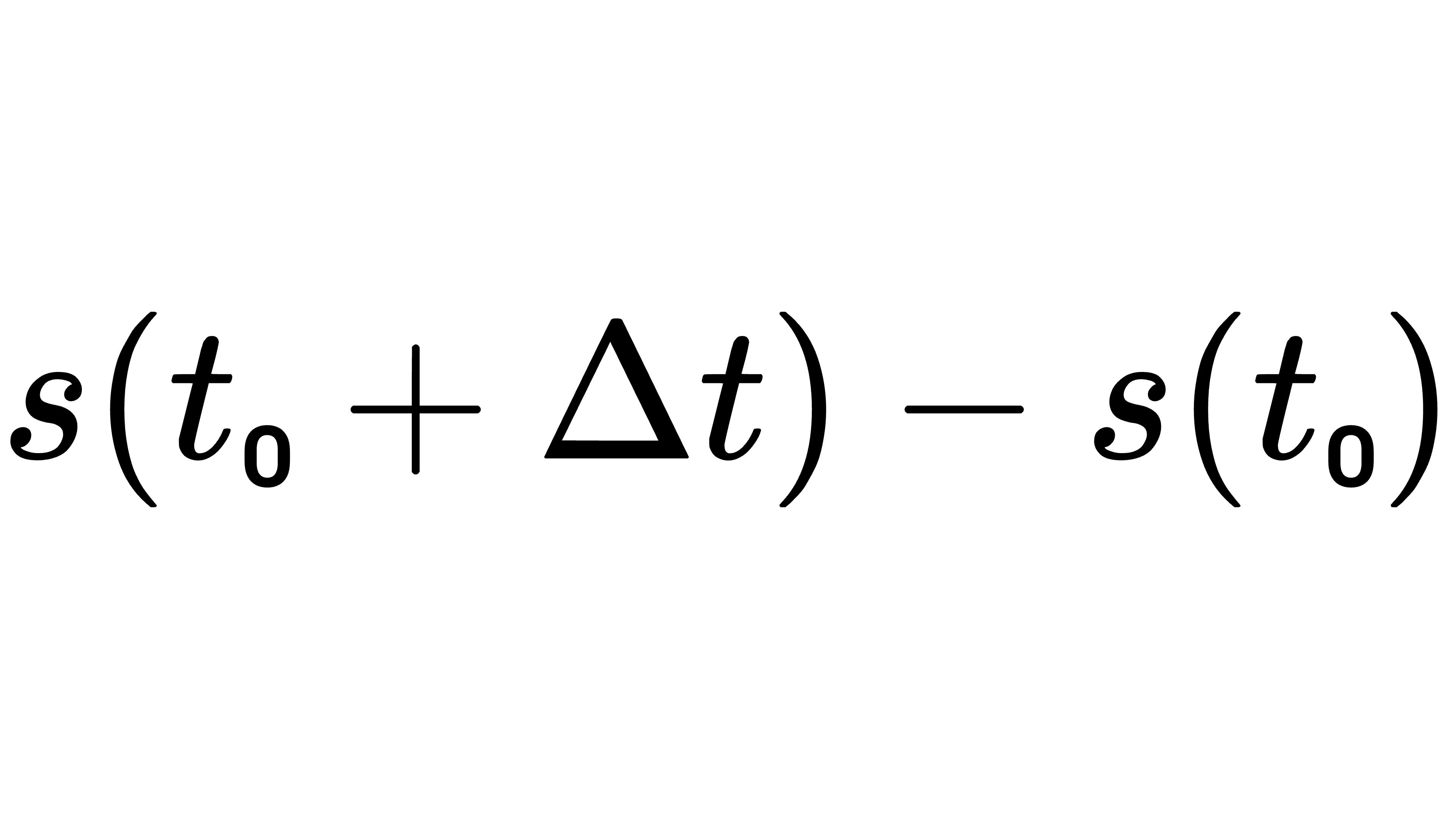
那么，这位普通男人在 Δt 这段时间内的平均速度为
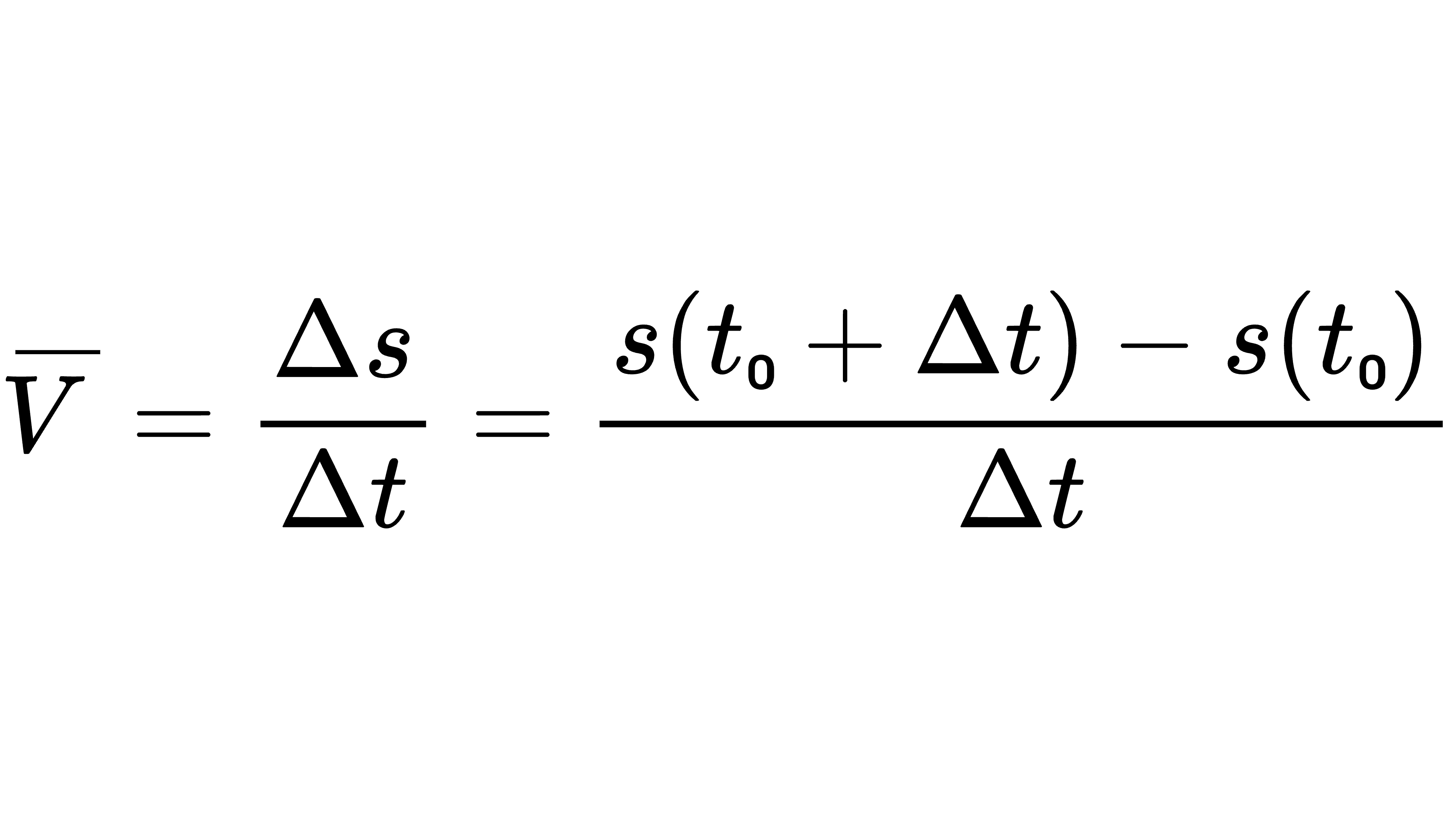
如果说这个普通男人做匀速直线运动，那么它在 Δt 这段时间内的平均速度
就是他在任意时刻的速度。但当他做变速直线运动时，他的速度随时间而确定，如果说当时间间隔 Δt 非常非常小时。我们可以近似的认为他在时间区间[t₀+Δt , t₀+Δt]内做匀速直线运动，所以就可以用作为他在t₀时刻的瞬时速度 v(t₀) 的近似值。显然， Δt 越小，这个近似程度越好。特别地，当 
时，将无限地接近于 v(t₀) ，即
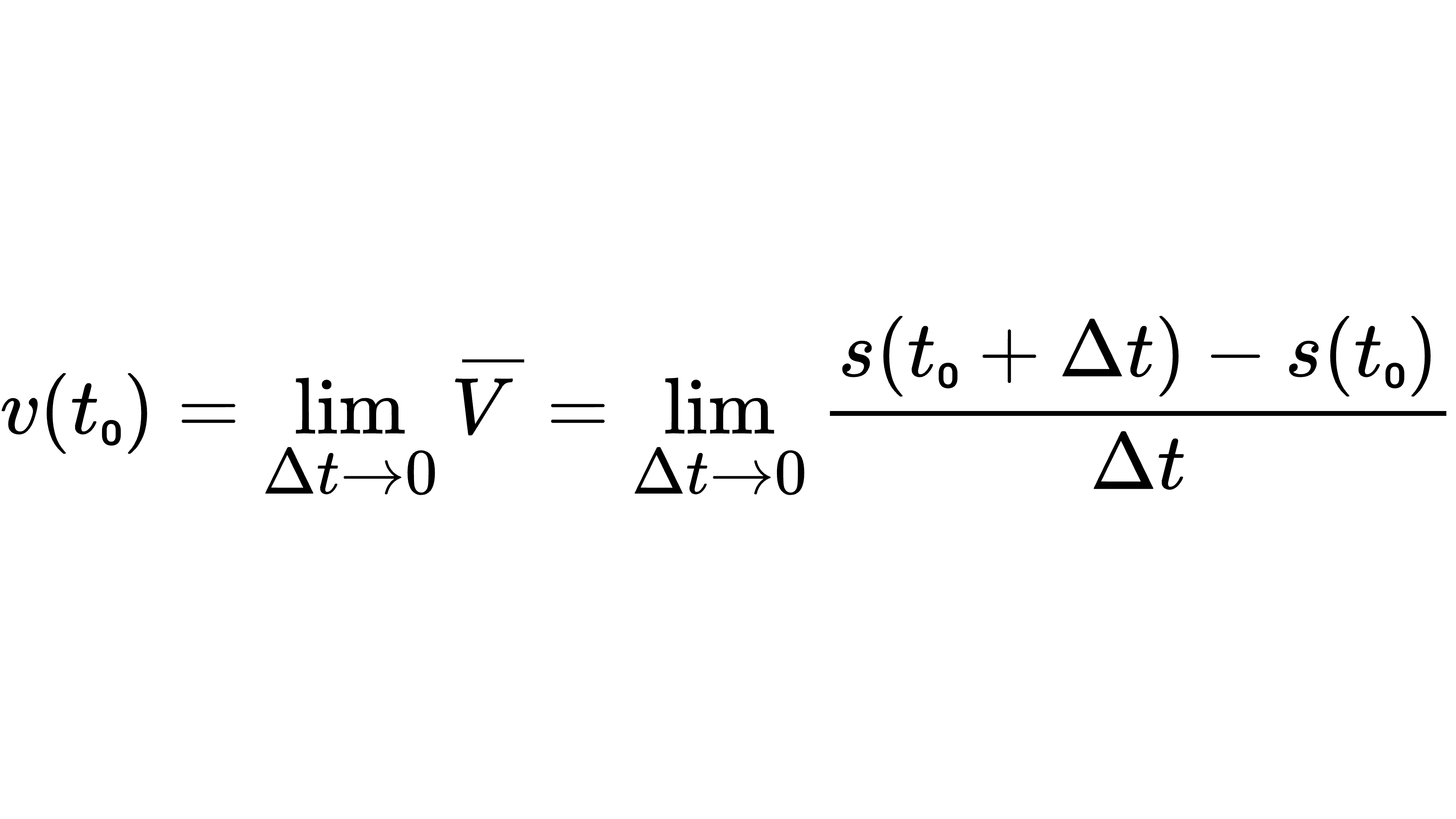
由此可见 v(t₀) 就是路程函数 s(t) 在 t=t₀ 点的变化率（在函数图像上体现为这点处切线的斜率，具体内容下次再讲）
相信大家对函数的变化率有一定的了解了，已经迫不及待想（学习）导（数）了罢。先忍一忍，下次就可以开始导了。
